(UPC, BGSMath), (UPC, IMTech), (ICMAT). Received 21 May, 2021.
Introduction
In the book The Emperor’s new mind [10], Sir Roger Penrose returns to the artificial intelligence debate to convince us that creativity cannot be presented as the output of a “mind” representable as a Turing machine. This idea, which is platonic in nature and highly philosophical, evolves into more tangible questions such as: What kind of physics might be non-computational?
The ideas of the book are a source of inspiration and can be taken to several landscapes and levels of complexity: Is hydrodynamics capable of performing computations? (Moore [9]). Given the Hamiltonian of a quantum many-body system, is there an algorithm to check if it has a spectral gap? (this is known as the spectral gap problem, recently proved to be undecidable [5]). And last but not least, can a mechanical system (including a fluid flow) simulate a universal Turing machine (universality)? (Tao [15–17]).
This last question has been analyzed in relation to the conjecture of the regularity of the Navier-Stokes equations [14], which is one of the unsolved problems in the Clay’s millennium list. In [18] Tao speculates on a connection between a potential blow-up of the Navier-Stokes equations and Turing completeness and fluid computation. It is interesting to mention that another of the one million dollars problem on the same list whose resolution is still pending is the P versus NP problem, which concerns the complexity of systems. Grosso modo, the question is whether any problem whose solution can be verified by an algorithm polynomial in time (“of type N P ”) can also be solved by another algorithm polynomial in time (“of type P ”). The delicate distinction between verification and solution has opened up an intricate scenery combining research in theoretical computer science, physics and mathematics. Although there is no apparent relation between the two celebrated problems in Clay’s list, understanding a fluid flow as a Turing machine may shed some light on their
connection.
On the other hand, undecidability of systems is everywhere and also on the invisible fine line between geometry and physics: As proven by Freedman [21], non-abelian topological quantum field theories exhibit the mathematical features (combinatorics) necessary to support an NP-hard model. This relates topological quantum field theory and the Jones polynomial (as described by Witten [19]) to the P 6 = N P problem. Other undecidable problems on the crossroads of geometry and physics are the stability of an n-body system [8], the problem of finding an Einstein metric for a fixed 4-fold as observed by Wolfram [20], ray tracing problems in 3D optical systems [12], or neural networks [13]. Fundamental questions at the heart of low dimensional geometry and topology such as verifying the equivalence of two finitely specified 4-manifolds [20], or the problem of computing the genus of a knot [2], have also been proven to be undecidable and NP-hard problems, respectively.
In [1] we addressed the appearance of undecidable phenomena in fluid dynamics and proved the existence of stationary solutions of the Euler equations on a Riemannian 3-dimensional sphere that can simulate any Turing machine (i.e., they are Turing complete). These solutions describe the dynamics of an inviscid and incompressible fluid in equilibrium. The type of flows that we consider are Beltrami fields, a particularly relevant class of steady Euler flows. Our novel strategy fusions the computational power of symbolic dynamics with techniques from contact topology and its connection with hydrodynamics unveiled by Sullivan, Etnyre and Ghrist more than two decades ago [6].
Euler equations and Beltrami fields
Euler equations model the dynamics of an incompressible fluid flow without viscosity. Even if they are classically considered on R^{3}, they can be formulated on any 3-dimensional Riemannian manifold (M, g) and follow the same mnemonics as the classical ones from vector calculus (for an introduction to the topic see [3, 11]). The equations can be written as:
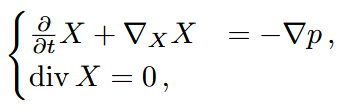
where p stands for the hydrodynamical pressure and X is the velocity field of the fluid (a non-autonomous vector field on M). Here ∇_{X} X denotes the covariant derivative of X along X. A solution to the Euler equations is called stationary whenever X does not depend on time, i.e., ∂/∂t X = 0.
The Euler equations can be defined in higher dimensions [3], an extension that is very useful to show that the steady Euler flows exhibit remarkable universality features as we proved in [4]. In this note, however, we shall restrict ourselves to 3-dimensional fluids.
Two fundamental notions
- A volume-preserving (autonomous) vector field X on M is Eulerisable if there exists a Riemannian metric g on M compatible with the volume form, such that X satisfies the
stationary Euler equations on (M, g):
- A divergence-free vector field X on (M, g) is called Beltrami if
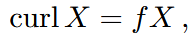with f ∈ C^{∞}(M). The classical Hopf fields on the 3-sphere S^{3} and the ABC flows on the 3-torus T^{3} are examples of Beltrami fields [11]
Turing machines
A Turing machine is a mathematical model of a theoretical device manipulating a set of symbols on a tape following some specific rules. It receives, as input data, a sequence of zeros and ones and, after a number of steps, returns a result, also in the form of zeros and ones. More concretely: A Turing machine is defined as T = (Q, q_{0}, q_{halt}, Σ, δ), where Q is a finite set of states, including an initial state q0 and a halting state q_{halt}, Σ is the alphabet, and δ : (Q × Σ) → (Q × Σ × {−1, 0, 1}) is the transition function. The input of a Turing machine is the current state q ∈ Q and the current tape t = (t_{n})_{n∈Z} ∈ Σ^{Z}.
How a Turing machine works. If the current state is q_{halt} then halt the algorithm and return t as output. Otherwise compute δ(q, t_{0}) = (q′, t′_{0}, ε), replace q with q′, t_{0} with t′_{0} and t by the ε-shifted tape.
The space of configurations is denoted by P := Q×Σ^{Z}. The global transition function ∆ : Q \ {q_{halt}} × Σ^{Z} → P (it sends a configuration in P to the configuration obtained after applying a step of the algorithm). A Turing machine is reversible if the global transition function ∆ is injective.
Native to the realm of computer science, the notion of Turing completeness in the title of the article [1] refers to a system that can simulate any Turing machine.
The halting problem. In computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will stop running (halting state), or continue to run forever. Alan Turing proved in 1936 that a general algorithm to solve the halting problem for all possible program-input pairs cannot exist. A key part of the proof is the formulation of a mathematical definition of a computer and program (the preceding notion of Turing machine), which allowed to prove that the halting problem is undecidable. The halting problem is historically important as it was one of the fir st problems to be proved undecidable.
Turing machines and universality. An Eulerisable field on M is Turing complete if it can simulate any Turing machine. In other words, the halting of any Turing machine with a given input is equivalent to a certain bounded trajectory of the field entering a certain open set of M.
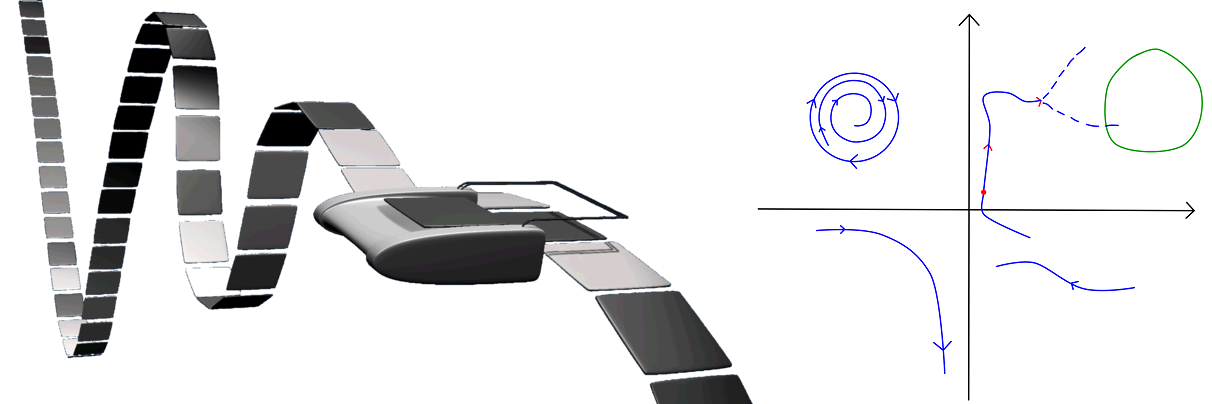
Turing machine and a Turing complete vector field associated to a point and an
open set.
A Turing machine can be simulated by a dynamical system (a vector field or a diffeomorphism).
Our construction
The construction that we provide in [1] can be understood as a mathematical theoretical fluid computer; it takes as input data a point in space, processes it –following the trajectory of the fluid through that point– and its outcome is the next region to which the fluid has moved. In the proof we use techniques from geometry, topology and dynamical systems developed over the last 30 years. Specifically, we combine symplectic and contact geometry and fluid dynamics with computer science theory and mathematical logic.
Geometry to the rescue. Beltrami fields have a strong geometrical flavour. In terms of the dual one-form α = ι_{X}g, and the volume form μ, the equation of Beltrami fields reads
When f does not vanish, the one-form α is a contact form (i.e., such that α∧dα ≠ 0) as observed longtime ago in [6]. One of the main characters of contact manifolds and the study of their dynamics are Reeb vector fields R, which are characterized by the conditions α(R) = 1 and ι_{R}dα = 0. In [6] it was also proved that any Reeb vector field defines a steady Euler flow for some ambient metric. This correspondence gives a mirror between contact geometry and Beltrami fields.
A key point of our construction lies in the following theorem, which we also prove in [1]:
Theorem 1 (A Reeb suspension) Let (M, ξ) be a contact 3-manifold and φ: D → D an area-preserving diffeomorphism of the disk which is the identity on (a neighborhood of) the boundary. Then there exists a defining contact form α whose associated Reeb vector field R exhibits a Poincaré section with first return map conjugated to φ.
A bit of symbolic dynamics. In 1991, Moore generalized the notion of shift to be able to simulate any Turing machine. Given a Turing machine there is a generalized shift ϕ conjugated to it. Conjugation means that there is an injective map φ : P → Σ^{Z} such that the global transition function of the Turing machine is given by ∆ = φ^{−1}ϕφ.
Key observation. Generalized shifts are conjugated to maps of the square Cantor set C^{2} := C × C ⊂ I^{2}, where C is the (standard) Cantor ternary set in the unit interval I = [0, 1].
Point assignment. Take Σ = {0, 1}. Given s = (…s_{−1} s_{0} s_{1}…) ∈ Σ^{Z}, we can associate to it an explicitly constructible point in the square Cantor set. We just express the coordinates of the assigned point in base 3: the coordinate y corresponds to the expansion (y_{0}, y_{1}, …) where yi = 0 if s_{i} = 0 and y_{i} = 2 if s_{i} = 1. Analogously, the coordinate x corresponds to the expansion (x_{1}, x_{2}, …) in base 3 where x_{i} = 0 if s_{−i} = 0 and x_{i} = 2 if s_{−i} = 1.
Moore proved that any generalized shift is conjugated to the restriction to the square Cantor set of a piecewise linear map of I^{2}. This map consists of finitely many area-preserving linear components defined on blocks. If the generalized shift is bijective, then the image blocks are pairwise disjoint. Each linear component is the composition of two linear maps: a translation and a positive (or negative) power of the horseshoe map.
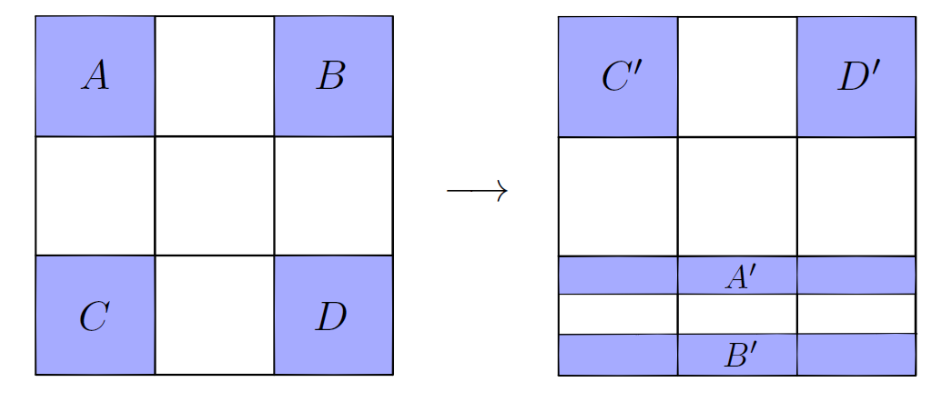
An example of a piece-wise linear map of the square.
In [1] we prove:
Proposition 2 For each bijective generalized shift and its associated map of the square Cantor set ϕ, there exists an area-preserving diffeomorphism of the disk φ : D → D which is the identity in a neighborhood of ∂D and whose restriction to the square Cantor set is conjugated to ϕ.
This allows us to assemble all the former pieces into the final construction.
End of the proof: On the other side of the mirror. Using the contact mirror, the Proposition above and Theorem 1 we can prove the main result in [1]:
Theorem 3 There exists an Eulerisable flow X on S^{3} that is Turing complete.
The metric g that makes X a stationary solution of the Euler equations can be assumed to be the round metric in the complement of an embedded solid torus (which is the region where the universal Turing machine is encoded).
Conclusions
Undecidability and chaos. Because of the undecidability of the halting problem for Turing machines, an important property of a Turing complete dynamical system is the existence of trajectories which exhibit undecidable long-term behavior. Specifically, it is undecidable to determine if the trajectory through an explicit point will intersect an explicit open set of the space.
One of the main consequences of the result is that it allows us to prove that certain phenomena of hydrodynamics are undecidable. That is, there is no algorithm to ensure that a fluid particle will pass through a certain region of space in finite time (in metaphoric terms: if we send a message inside a bottle, we cannot guarantee that it will reach its recipient). This inability to predict, which is different from that established by chaos theory, can be understood as a new manifestation of the turbulent behaviour of fluids.
In chaos theory, unpredictability is associated with the extreme sensitivity of the system to the initial conditions –the flutter of a butterfly can generate a tornado–, whereas we prove that there can be no algorithm that solves the problem, so that it is not a limitation of our knowledge, but of the mathematical logic itself.
Theoretical fluid computers and the Navier–Stokes problem. TaoTao, T. launched a program in 2016 [14–18] based on the Turing completeness of the Euler equations to address the blow up problem for the Navier-Stokes equations included in the Clay Foundation’s list of Millennium Problems. Tao’s proposal is, at the moment, speculative. The idea of Tao is to use a Theoretical fluid computer to force the fluid to accumulate more and more energy in smaller regions, until a singularity is formed, that is, a point at which the energy becomes infinite. However, at the moment it is widely open how to do this for the Euler or Navier–Stokes equations.
References
[1] R. Cardona, E. Miranda, D. Peralta-Salas, F. Presas. Constructing Turing complete Euler flows in dimension 3. Proceedings of the National Academy of Sciences May 2021, 118 (19) e2026818118; DOI: 10.1073/pnas.2026818118.
[2] I. Agol, J. Hass, W. Thurston. The computational complexity of knot genus and spanning area. Trans. Amer. Math. Soc. 358 (2006) 3821–3850.
[3] V. I. Arnold, B. Khesin. Topological Methods in Hydrodynamics. Springer, New York, 1999.
[4] R. Cardona, E. Miranda, D. Peralta-Salas, F. Presas. Universality of Euler flows and flexibility of Reeb embeddings. Preprint (2019) arXiv:1911.01963.
[5] T. Cubitt, D. Perez-Garcia, M. Wolf. Undecidability of the spectral gap. Nature 528 (2015) 207–211.
[6] J. Etnyre, R. Ghrist. Contact topology and hydrodynamics I. Beltrami fields and the Seifert conjecture. Nonlinearity 13 (2000) 441–458.
[7] M. Freedman. P/NP, and the quantum field computer. Proc. Natl. Acad. Sci. USA 95 (1998) 98–101.
[8] C. Moore. Undecidability and Unpredictability in Dynamical Systems. Phys. Rev. Lett. 64 (1990) 2354–2357.
[9] C. Moore. Generalized shifts: unpredictability and undecidability in dynamical systems. Nonlinearity 4 (1991) 199–230.
[10] R. Penrose. The emperor’s new mind. Concerning computers, minds, and the laws of physics. With a foreword by Martin Gardner. The Clarendon Press, Oxford University Press, New York, 1989. xiv+466 pp. ISBN: 0-19-851973-7.
[11] D. Peralta-Salas. Selected topics on the topology of ideal fluid flows. Int. J. Geom. Methods Mod. Phys. 13 (2016), suppl., 1630012, 23 pp.
[12] J.H. Reif, J.D. Tygar, A. Yoshida. Computability and complexity of ray tracing. Discrete Comput. Geom. 11 (1994) 265–288.
[13] H.T. Siegelmann, E.D. Sontag. On the computational power of neural nets. J. Comput. Syst. Sci. 50 (1995) 132–150.
[14] T. Tao. Finite time blowup for an averaged three-dimensional Navier-Stokes equation. J. Amer. Math. Soc. 29 (2016), no. 3, 601-674.
[15] T. Tao. On the universality of potential well dynamics. Dyn. PDE 14 (2017) 219-238.
[16] T. Tao. On the universality of the incompressible Euler equation on compact manifolds. Discrete and Continuous Dynamical Systems – A (2018) 38 (3) : 1553-1565.
[17] T. Tao. On the universality of the incompressible Euler equation on compact manifolds, II. Nonrigidity of Euler flows. Preprint arXiv:1902.0631 (2019).
[18] T. Tao. Searching for singularities in the Navier-Stokes equations. Nature Reviews Physics 1 (2019) 418–419.
[19] E. Witten. Quantum field theory and the Jones polynomial. Comm. Math. Phys. 121 (1989) 351–399.
[20] S. Wolfram. Undecidability and intractability in theoretical physics. Phys. Rev. Lett. 54 (1985) 735–738.
[21] M. Freedman. P/NP, and the quantum field computer. Proc. Natl. Acad. Sci. 95 (1998) 98–101.