(FWO-KU Leuven) Received 21 April, 2022.
The paper [3] solves a long-standing conjecture about the structure of the roots of the Bernstein-Sato polynomial for plane branches posed by T. Yano in 1982 [18].
Let f : (C^{n+1}, 0) −→ (C, 0) be a germ of a holomorphic function. To each such germ, one can associate a functional equation
between the symbolic powers f^{s} of f. Here,
is a polynomial in the variable s and having coefficients in the ring of differential operators C{x_{0}, . . . , x_{n}}⟨∂_{0}, . . . , ∂_{n}⟩.
The set of all polynomials b_{f,P} (s) appearing in (1) forms an ideal of C[s]. The monic generator of this ideal is called the Bernstein-Sato polynomial b_{f}(s) of f and it is an invariant of the singularities of the zero set f^{−1}(0).
The roots of bf (s) are known to be negative rational numbers contained in the interval (−n − 1, 0) [9, 15] and are related with many other invariants of the singularities as the monodromy eigenvalues, the jumping numbers or the spectrum of the singularity [5, 14]. In contrast with all these invariants, the Bernstein-Sato polynomial is not a topological invariant, that is, it depends on the equation defining f.
In this context, Yano’s conjecture predicts that in the case n = 1 and if f is irreducible the roots of b_{f}(s) are completely determined by the topological type if f is generic enough. For the precise statement see Conjecture 1 below. Moreover, Yano’s conjecture predicts the value of all the roots of bf (s) from topological invariants.
In order to state Yano’s conjecture we first need a characterization of the Bernstein-Sato polynomial in terms of the Gauss-Manin connection of f. Assume that f: (C^{n+1}, 0) −→ (C, 0) has an isolated singularity at the origin. Let
the Milnor number of f, which is finite since f has an isolated singularity. Consider the Brieskorn lattice of f
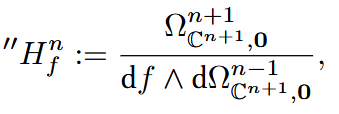
which is a free C{t}–module of rank μ, where the action of t is given by multiplication by f. In addition, it carries a covariant derivative ∂_{t} that coincides with the Gauss-Manin connection of the singularity.
Theorem 1 (Malgrange [13]). Let
the saturation of the Brieskorn lattice 
. The reduced Bernstein-Sato polynomial 
of an isolated singularity f coincides with the minimal polynomial of the action
Notice that the last morphism is an endomorphism of complex vector spaces of dimension μ. Then, one defines the b-exponents of f as the roots of the characteristic polynomial of the action of 
This way, there are always μ b-exponents counted with possible multiplicities.
Let now f : (C^{2}, 0) −→ (C, 0) be an irreducible plane curve. For this type of singularities, the topological type of the singularity is completely determined by a tuple of positive integers (n, β_{1}, . . . , β_{g}), g ≥ 1, called the characteristic sequence. From this data, define
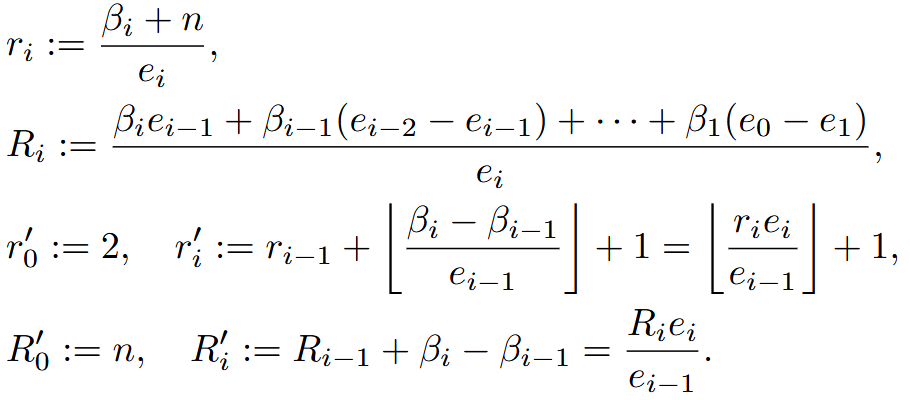
Conjecture 1 (Yano [18]). For generic fibers of some μ–constant deformation of f, the b-exponents {α_{1}, . . . , α_{μ}} are given by the generating sequence
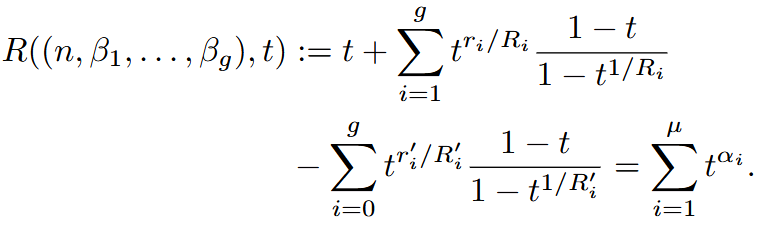
In this context a μ–constant deformation is the same as topologically trivial deformation.
Yano’s conjecture was proven in the case where g = 1 by Cassou-Noguès [6]. The case g = 2 was proved by Artal-Bartolo, Cassou-Noguès, Luengo and Melle-Hernández [1] under the assumption that the eigenvalues of the monodromy are pair-wise different. Under this same assumption, we gave a proof for any g ≥ 1 in [2].
We will now give a short overview of the proof for the general case. The main idea is to study the asymptotic expansion of periods in the Milnor fiber.
Let 
be a Milnor representative of a germ 
. Let X_{t},t ∈ T \ {0} be the Milnor fiber of f. Let ω a section of 
and γ(t) a cycle in X_{t} that vanishes to zero as t → 0, then one has
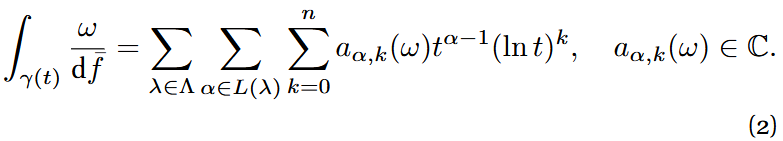
where 
is the Gel’fand-Leray form, Λ is the set of eigenvalues of the monodromy of f and 
The period integrals have such an expansion because they are solutions to the Gauss-Manin connection which has regular singularities [4, 12].
The b-exponents of f appear as a subset of the exponents of the period integrals from (2), hence the name. A theorem of Varchenko [17] gives the necessary conditions under which a_{α,k}(ω) ≠ 0 implies that α is a b-exponent.
The relation between the candidates from Yano’s conjecture and the asymptotic expansions comes from resolution of singularities. It turns out that the numerical data considered by Yano’s conjecture can be interpreted in terms of the numerical data appearing in a resolution of singularities of f.
The main technical result in [3] is the construction of the asymptotic expansions from (2) in terms of the resolution of singularities of f. This generalizes previous results of Varchenko, Lichtin and Loeser [10, 11, 17] where only the first terms were considered. Although such construction is possible for any germ f, conditions under which a_{α,k} ≠ 0 are much harder to obtain. However, such results are known for the case of plane curves after a result of Deligne and Mostow [7]. In general, understanding the non-vanishing of the coefficients a_{α,k}(ω) is an open problem that is related to the Strong Monodromy Conjecture [8].
The last part of the proof is devoted to constructing the particular μ–constant deformation predicted in Conjecture 1. To achieve that we make use of a classical object in the theory of curve singularities, Teissier’s monomial curve and its deformation [16]. This part of the proof only works under the assumption that f is irreducible.
References
[1] E. Artal Bartolo, P. Cassou-Noguès, I. Luengo, and A. Melle Hernández. Yano’s conjecture for two-Puiseux-pair irreducible plane curve singularities. Publ. Res. Inst. Math. Sci., 53(1):211–239, 2017.
[2] G. Blanco. Poles of the complex zeta function of a plane curve. Adv. Math., 350(9):396–439, 2019.
[3] G. Blanco. Yano’s conjecture. Invent. Math., 226:421–465, 2021.
[4] E. Brieskorn. Die Monodromie der isolierten Singularitäten von Hyperflächen. Manuscripta Math., 2:103–161, 1970.
[5] N. Budur and M. Saito. Multiplier ideals, V -filtration, and spectrum. J. Algebraic Geom., 14(2):269–282, 2005.
[6] P. Cassou-Noguès. Polynôme de Bernstein générique. Abh. Math. Semin. Univ. Hambg., 58(1):103–124, 1988.
[7] P. Deligne and G. D. Mostow. Monodromy of hypergeometric functions and nonlattice integral monodromy. Inst. Hautes Études Sci. Publ. Math., 63:5–89, 1986.
[8] J. Igusa. B-functions and p-adic integrals. In M. Kashiwara and T. Kawai, editors, Algebraic analysis, volume 1, pages 231–241. Academic Press, Boston, MA, 1988.
[9] M. Kashiwara. B-functions and holonomic systems. Invent. Math., 38(1):33–53, 1976.
[10] B. Lichtin. Poles of |f (z, w)|^{2s} and roots of the B-function. Ark. Mat., 27(1-2):283–304, 1989.
[11] F. Loeser. Fonctions d’Igusa p-adiques et polynômes de Bernstein. Amer. J. Math., 110(1):1–21, 1988.
[12] B. Malgrange. Intégrales asymptotiques et monodromie. Ann. Sci. École Norm. Sup. (4), 7(3):405–430, 1974.
[13] B. Malgrange. Le polynôme de Bernstein d’une singularité isolée. Lecture Notes in Math., 4:98–119, 1975.
[14] B. Malgrange. Polynôme de Bernstein-Sato et cohomologie évanescente. In Analysis and topology on singular spaces, II, III, volume 101-102 of Astérisque, pages 243–267, Paris, 1983. Soc. Math. France.
[15] M. Saito. On microlocal b-function. Bull. Soc. Math. France, 122:163–184, 1994.
[16] B. Teissier. Appendix. 1986. in [19].
[17] A. N. Varchenko. Asymptotic Hodge structure in the vanishing cohomology. Math. USSR-Izv., 18(3):469–512, 1982.
[18] T. Yano. Exponents of singularities of plane irreducible curves. Sci. Rep. Saitama Univ. Ser., 10(2):21–28, 1982.
[19] O. Zariski. Le problème des modules pour les branches planes. Hermann, Paris, 1986.