(LaCàN, IMTech). Received on November 27th, 2022.
Cell migration is a mechanical function central to life. It establishes how cells move and interact during development to eventually form fully functional organs. When this fascinating and yet obscure interaction of genetics, chemistry and physics evolves normally, our brain, heart, liver, etc., work in perfect cooperation. Consequently the body performs without complains. A fascinating property of organ development is that it is extremely robust. If we consider the possibilities of the number of alterations in human development that could occur due to abnormal cell and tissue function, and that eventually most of the organs develop without an issue, we will appreciate how exceptional our body is. The equally robust cell migration is not only the very essence of a successful organ development but it is also important for regenerative properties of damaged tissues and organs.
Unfortunately, the robustness of biological systems has also important drawbacks. For example, cell migration is responsible for the invasion of cancer cells from of the tumor niche toward healthy tissues, through the blood or lymph system. Similar to the development and regeneration of tissues, tumor cell invasion is a very robust process. When this happens, the tumor has metastasized. This is a dramatic stage in cancer progression, because when tumor cells leave the primal tumor and advance to other tissues and organs, cancer is hard to control.
Traditionally, experimental work has taken the reins in the study of cell, tissue and organ biology. This was also the case for cell migration. However, mathematicians, physicists and engineers have been very active during the last decades to build accurate mathematical models that explain experimental observations and provide new insights on how cells migrate. Most mathematical models of cell migration have relied on three key cellular structures associated with basic mechanical processes (see Figure). Cells are made of a dynamic cytoskeleton network encapsulated in the cell membrane. One of these networks, the actin network, is directly involved in cell migration. The actin network continuously polymerizes and pushes the cell membrane outward. This is the first structure associated with cell migration. A second distinctive actin network combines with myosin motors, molecules that link two actin filaments and pull on them, to create an active viscoelastic. This acto-myosin network, also named retrograde flow, flows inward from the cell boundary. The result of these two competing actin networks, one moving outward and the other inwards, determine the direction and velocity of cell migration. Cells also create cell adhesions, clusters of molecules that link the intracellular acto-myosin network with the extracellular matrix (ECM), to sense their mechanical environment. Moreover, cell adhesion dynamics depends on how these molecules sense and respond to the mechanical properties of the ECM and determines how cell adhesions form and disassemble. In physical terms, cell adhesion creates friction between the cell and the ECM.
But then, how does a cell determine the direction of migration? How does a cell organize itself to migrate in a specific direction during development, regeneration or cancel invasion? Without a stimulus that can break the symmetry in all the mechanical mechanisms described above, cells would spread symmetrically but they would not migrate. Cells follow signals of very different nature that are self-generated or exogenous.
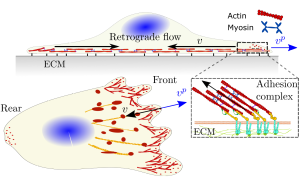
Figure. Sketch of the cell system. Main mechanisms acting in
cell migration: cell adhesion, retrograde flow and polymerization of
actin against the cell membrane. vp (blue arrows) and v (black arrows)
are the polymerization and retrograde flow velocities.
For example, cells move guided by chemical and mechanical signals, in-vivo and in-vitro. In an environment where chemical gradients exist, different types of molecules that can cross the cell membrane feel the slightest of chemical gradients that exist around the cell body. Then, the cell activates intracellular chemical signals and polarize following the external chemical gradient. These chemical signals modify the activity of actin polymerization or myosin activity and, therefore, leads to a cell polarization in terms of the acto-myosin activity. Eventually, the acto-myosin polarization determines the directed cell migration during chemotaxis. Similarly, when the ECM in which a cell is embedded presents gradients of its mechanical properties, the cell senses it through the cell adhesion molecules. If one side of a cell is located in a stiff region but other side is on a softer one, the formation and strength of the cell adhesions, and consequently cell-ECM friction, would differ at different regions of the cell. As a result, the intracellular flow on the stiffer region will be different than the one on the softer region and this asymmetry would make the cell to undergo directed cell migration.
In the LaCàN, we have developed a number of mathematical models to study cell migration. Some of the simplest models, but still comprehensive enough to study cell migration, are those based on active gel theory [1]. We can also simplify the model assuming a 1D domain Ω moving in time with coordinates x(t) ∈ [lr(t), lf(t)]. lr(t) and lf(t) represent the rear and front boundary of the cell. These class of models determine the actin flow velocity v by solving balance of linear momentum in the following form
![]()
This balance assumes a viscous behavior of the actomyosin network, μ∂_{x}v, introduces the active contractility of myosin motors, ζ, and the cell-ECM friction, η, generated by the formation of cell adhesions. The acto-myosin network that forms at the cell-ECM contact plane usually flows inward, from the cell periphery toward the cell nucleus. The actin network that polymerizes against the cell membrane has a maximum polimerization velocity v_{p}^{0} when the cell membrane is under no tension. When the cell membrane builds up in tension, which occurs during the first stages of cell migration, the polymerization velocity, v_{p}, decreases proportionally to the opposing tension of the membrane point-wise. The outward polymerization velocity, v_{p}, competes with the inward retrograde flow velocity, v, to expand or retract the cell periphery (Figure). Active gel models also introduce mass transport of the intracellular. We can quantify the network density ρ(x, t) as
![]()
where f (ρ) = (wρ − ν∂_{x}ρ). The network velocity drags the cytoskeleton with velocity w in the cell frame of reference, diffuses and turnover with polymerization and depolymerization rates k_{p} and k_{d}. Different types and values of boundary conditions can be imposed to Eq. 4 and 5 to model specific phenomena. By coupling these basic equations, we can quantify what are the precise mechanical forces required for the cell to migrate and thus analyze how exogenous stimuli may induce a directed cell migration.
Recently, we have studied durotaxis, the directed cell migration toward stiffness gradients, through a mathematical model. A key aspect of our research was to couple stochastic clutch models, which describe the dynamic behavior of cell adhesions) [2] into the active gel theory. This model allowed us to explain how certain cell types migrate toward positive gradients of the ECM stiffness while others do it toward negative gradients. With an extension of this previous model of durotaxis, we have also studied how cells sense and react to chemical stimulito, eventually, migrate toward chemical gradients. More importantly, we analyzed how these two chemical and mechanical stimuli compete with each other [3]. This is a very important aspect in cell migration because, in in-vivo and in-vitro, cells are usually in complex mechano-chemical context, where both signals, at a smaller or larger degree, coexist.
We have also used these models to address how tumor cells may escape the tumor mass and invade other tissues, within the Mechano-control Project (FET proactive). During cancer progression, the ECM experiences mechanical changes, which are induced by the cell themselves. As a consequence, the cell adhesion changes, and so the cell-ECM friction does [4]. These adhesion changes induce remodeling of the intracellular network which trigger an oncogenic response. These changes in the ECM mechanics and in cell adhesion are critical in the invasiveness of tumor cells. Essentially, this change resembles the mechanism of durotaxis. Clearly, the impact of understanding the mechanical interactions between the cell and the ECM works is huge, because, if we understand how tumor cells migrate, we could Nevertheless, the implications of understanding how cells
migrate goes further than in life sciences. It also has an important impact in engineering. Throughout its history, engineering has generally used manufactured materials to build solutions such as airplanes, robots or electronic devices. While many of these engineering designs were somewhat bio-inspired, they are still far from achieving some of the unique functionalities of living organisms. Think, for example, on the robustness of our heart or the maneuverability of an eagle compare to jet aircrafts. Recent technologies have used assemblies of artificial materials and biological tissues to recapitulate more closely certain behaviors of biological systems. This technology has been used for the design of bio-hybrid soft-robots, that, e.g., imitate the movement of octopus arms, and for the design of grafts to support cardiac function. If we learn how to manipulate the directed cell migration, it may be the first step to engineer novel tissue constructs that form autonomously and that, upon formation, closely resembles the biological system they were intended to imitate. design strategies for arresting tumor cell invasion.
References
[1] J. Prost, F. Jülicher, J. F. Joanny, Active gel physics, Nature Physics 11 (2) (2015) 111–117.
[2] P. Sáez, C. Venturini Positive, negative and engineered durotaxis, bioRxiv 2022.09.26.508682.
[3] J. Betorz, G.R. Bokil, S.M. Deshpande, S. Kulkarnic, D. Rolando, C. Venturini, P. Saez A full computational model of cell motility: Early spreading, cell migration and competing taxis, bioRxiv 2022.09.28.509519.
[4] Z. Kechagia, P. Sáez, M. Gómez-González, M. Zamarbide, I. Andreu, T. Koorman, A.E.M. Beedle, P.W.B. Derksen, X. Trepat, M. Arroyo, P. Roca-Cusachs. The laminin-keratin link shields the nucleus from mechanical deformation and signalling, bioRxiv 2022.03.01.482474.