(Instituut-Lorentz, Leiden). Received on 4/12/2022.
Quantum mechanics allows for correlations that cannot be explained within two principles that are fundamental to our intuitive understanding of the world: locality and realism [1]. This led to Einstein and collaborators to wonder whether quantum mechanics was a complete theory for the description of reality [2]. Albeit these discussions remained pretty much on the philosophical plane, John S. Bell eventually formalized them via the introduction of a local hidden variable model (LHVM) [3]. Quantum correlations that do not admit a LHVM are termed nonlocal. Nonlocal correlations are revealed through the viola-
tion of a so-called Bell inequality. Incidentally, this year’s Nobel Prize in Physics rewarded the efforts of Aspect [4], Clauser[5] and Zeilinger [6, 7] for experiments with entangled photons, es tablishing the violation of Bell inequalities and pioneering quantum information science.
An LHVM is defined through an experiment where n space-like separated parties perform measurements on their laboratories and record their outcomes. Their measurement choices should be statistically independent of the internal state of the system being measured. Space-like separation prevents communication of the measurement choices to each other. We then expect to observe correlations of the form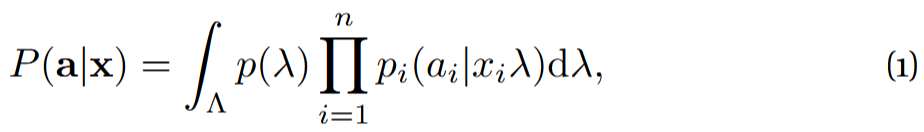
where P (a|x) denotes the probability that the i-th party observed outcome ai given that they performed the x_{i}-th measurement. Since parties are not allowed to communicate during
the experiment, but may have done so in the past (an interaction which is encoded in the so-called hidden variable λ ∈ Λ), we expect their individual responses to be independent if con-
ditioned on λ. Although we do not even define in which space λ may live, this is integrated out in Eq. (1).
Geometrically speaking, LHVM correlations form a convex polytope, denoted by ℙ. Its facets correspond to tight Bell inequalities and its vertices v_{i} are enumerated by all local deterministic strategies (LDSs); i.e., when each p_{i}(a_{i}|x_{i}, λ) is a Kronecker delta [8]. The vertices are straightforward to generate, but finding a minimal complete set of Bell inequalities is extremely costly [9] requiring use of the dual description method, which scales as O(V^{⌊D/2⌋}), where V = |{v_{i}}_{i}| is the number of vertices and D the ambient space dimension in which ℙ is embedded [10]. In a Bell experiment with n parties,
m measurement choices per party and d possible outcomes per measurement, V = d^{nm} and D = (1 + m(d − 1))^{n} − 1, which makes the task of obtaining all Bell inequalities intractable except for the simplest scenarios [11].
One might try to balance complexity and expressivity by focusing on Bell inequalities of a particular form [12, 13], further adapting them to overcome experimental limitations [14]. A
natural choice is to look for Bell inequalities invariant under the action of a symmetry group G; e.g., permutationally invariant Bell inequalities (PIBIs), where 
[15]. That requires characterizing the projected polytope ℙ^{G} := π(ℙ) onto the G-invariant subspace, where
The projection π naturally induces a partition of the multipartite LDSs into disjoint orbits, through the action of the symmetry group G. Via Pólya’s enumeration theorem, there are 
classes, where c counts the number of disjoint cycles of σ. The latter is an upper bound on the number of projected vertices, since π needs not preserve
extremality [16].
In the case of , the orbits are enumerated by partitions of n into dm elements. For convenienece, let us denote c ⊢ n such a partition, where c_{i} (with i = i_{1} . . . i_{m} encoded in base d) denotes how many parties choose the strategy that maps the j-th measurement to the i_{j} -th outcome [15]. At every LDS correlations behave deterministically, forming Boole algebra [17]. At the level of Eq. (1), this means that 
This factorization is also reflected at the level of 
where the 
-symmetric k-body marginals are k-degree polynomials in R[c] [15, 18].
Although the computational complexity of 
is greatly reduced, the number of vertices is now upper bounded by 
and if we further restrict to the space of at most k-body correlators, denoted 
, then D = O(poly(k)), the doubly-exponential scaling of the double-description method still prohibits a complete description for moderate values of n in practice.
Since is the convex hull of the points whose coordinates are expressed via elements of ℝ[c], when evaluated at partitions of n, one may further relax this condition to gain in terms of computational efficiency, at the expense of losing a bit in terms of resolution. In this case, the condition 
can be relaxed to c_{i} ∈ R. This transforms the problem of finding the convex hull of a finite number of points to that of finding the convex hull of a semialgebraic set that interpolates through the original one when c ⊢ n. That semialgebraic set is defined through the ideal resulting from the polynomial equations satisfied at LDSs, and the equality and inequality constraints inherited from c ⊢ n
[19].
The membership problem in the convex hull of a semialgebraic set is NP-hard in general, but approximations exist through semidefinite programs (SDP) [20, 21]. In particular, via
the so-called moment problem formulation [22, 23], the following SDP
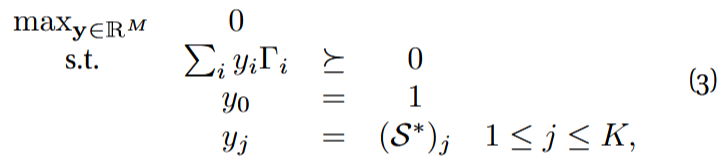
where K < M and Γ_{i} are symmetric matrices encoding the semialgebraic set relations, can quickly certify (in O(1) complexity with respect to n) if the experimental correlations, encoded in the vector S∗, lie outside the convex hull of the semialgebraic set [19]: if the SDP (3) is infeasible, it yields a certificate through its dual formulation. Such a certificate is
the Bell inequality that the experimental data S∗ violates. The Bell inequality coefficients and classical bound correspond to the dual variables associated to the equality constraints in (3). This method has successfully bypassed the polytope approach already in mesoscopic systems (500 ≲ n ≲ 5 · 105) [14, 24]. A natural next step is its application to find Tsirelson’s bounds to multipartite inequalities (what is the maximal quantum violation that Nature allows for a Bell inequality), where the polynomials are non-commutative [25], yielding operator-sum-of-squares decompositions applicable to self-testing [26]. Under certain conditions, the latter allows to certify, just from the observed statistics, which quantum states and measurements (up to unobservable degrees of freedom) must have generated
them.
References
[1] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, and Stephanie Wehner, Bell nonlocality, Rev. Mod. Phys. 86 (2014), 419–478.
[2] Albert Einstein, B. Podolsky, and N. Rosen, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Phys. Rev. 47 (1935), 777–780.
[3] John Stewart Bell, On the Einstein Podolsky Rosen paradox, Physics 1 (1964), 195–200.
[4] Alain Aspect, Philippe Grangier, and Gérard Roger, Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities, Phys. Rev. Lett. 49 (1982), 91–94.
[5] John F. Clauser, Michael A. Horne, Abner Shimony, and Richard A. Holt, Proposed Experiment to Test Local Hidden-Variable Theories, Phys. Rev. Lett. 23 (1969), 880–884.
[6] Dik Bouwmeester, Jian-Wei Pan, Klaus Mattle, Manfred Eibl, Harald We infurter, and Anton Zeilinger, Experimental quantum teleportation, Nature 390 (1997), no. 6660, 575–579.
[7] Jian-Wei Pan, Dik Bouwmeester, Matthew Daniell, Harald Weinfurter, and Anton Zeilinger, Experimental test of quantum nonlocality in three-photon Greenberger–Horne–Zeilinger entanglement, Nature 403 (2000), no. 6769, 515–519.
[8] Arthur Fine, Hidden Variables, Joint Probability, and the Bell Inequalities, Physical Review Letters 48 (1982), no. 5, 291–295.
[9] Laszlo Babai, Lance Fortnow, and Carsten Lund, Non-deterministic exponential time has two-prover interactive protocols, Computational Complexity 1 (1991), no. 1, 3–40.
[10] Bernard Chazelle, An optimal convex hull algorithm in any fixed dimension, Discrete & Computational Geometry 10 (1993), no. 4, 377–409.
[11] Cezary ´Sliwa, Symmetries of the Bell correlation inequalities, Physics Letters A 317 (2003), no. 3, 165 – 168.
[12] J. Tura, R. Augusiak, A. B. Sainz, T. Vértesi, M. Lewenstein, and A. Acín, Detecting nonlocality in many-body quantum states, Science 344 (2014), no. 6189, 1256–1258, available at http://science.sciencemag.org/ content/344/6189/1256.full.pdf.
[13] J. Tura, G. De las Cuevas, R. Augusiak, M. Lewenstein, A. Acín, and J. I. Cirac, Energy as a Detector of Nonlocality of Many-Body Spin Systems, Phys. Rev. X 7 (2017), 021005.
[14] Roman Schmied, Jean-Daniel Bancal, Baptiste Allard, Matteo Fadel, Valerio Scarani, Philipp Treutlein, and Nicolas Sangouard, Bell correlations in a Bose-Einstein condensate, Science 352 (2016), no. 6284, 441–444, available at http://science.sciencemag.org/content/352/6284/441.full.pdf.
[15] J. Tura, R. Augusiak, A.B. Sainz, B. Lücke, C. Klempt, M. Lewenstein, and A. Acín, Nonlocality in many-body quantum systems detected with two-body correlators, Annals of Physics 362 (2015), 370 – 423.
[16] Günter M. Ziegler, Lectures on Polytopes, Springer New York, 1995.
[17] Itamar Pitowsky and Karl Svozil, Optimal tests of quantum nonlocality, Phys. Rev. A 64 (2001), 014102.
[18] Albert Aloy, Matteo Fadel, and Jordi Tura, The Quantum Marginal Problem for Symmetric States: Applications to Variational Optimization, Nonlocality and Self-Testing, New Journal of Physics (2021).
[19] Matteo Fadel and Jordi Tura, Bounding the Set of Classical Correlations of a Many-Body System, Phys. Rev. Lett. 119 (2017), 230402.
[20] João Gouveia, Pablo A. Parrilo, and Rekha R. Thomas, Theta Bodies for Polynomial Ideals, SIAM Journal on Optimization 20 (2010), no. 4, 2097–2118.
[21] Grigoriy Blekherman, Pablo A. Parrilo, and Rekha Thomas (eds.), Semidefinite Optimization and Convex Algebraic Geometry, SOC FOR INDUSTRIAL & APPLIED M, March 21, 2013.
[22] Jean B. Lasserre, Global Optimization with Polynomials and the Problem of Moments, SIAM Journal on Optimization 11 (2001), no. 3, 796-817, available at https://doi.org/10.1137/S1052623400366802.
[23] João Gouveia and Rekha R. Thomas, Chapter 7: Spectrahedral Approximations of Convex Hulls of Algebraic Sets, Semidefinite Optimization and Convex Algebraic Geometry, 2012, pp. 293–340.
[24] Nils J. Engelsen, Rajiv Krishnakumar, Onur Hosten, and Mark A. Kasevich, Bell Correlations in Spin-Squeezed States of 500 000 Atoms, Phys. Rev. Lett. 118 (2017), 140401.
[25] Miguel Navascués, Stefano Pironio, and Antonio Acín, Bounding the Set of Quantum Correlations, Phys. Rev. Lett. 98 (2007), 010401.
[26] Ivan Šupi´c and Joseph Bowles, Self-testing of quantum systems: a review, Quantum 4 (2020), 337.