(UPC) and (UB, CRM). Received November 28, 2023.
Consider the N -body problem, namely the motion of N bodies in 3-dimensional space subject to the Newtonian universal attraction:
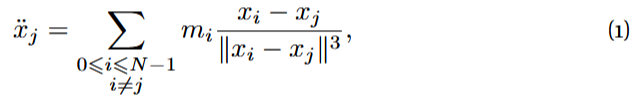
where x_{j} ∈ ℝ^{3} is the position and m_{j} > 0 the mass of body j. Of particular interest is the planetary problem, where the masses of bodies 1, . . . , N − 1 (the planets) are small with respect to the mass of body 0 (the sun). Since the masses of the planets are so small, the gravitational planet-planet interaction is much weaker than the attraction of the planets to the sun.
If one neglects the planet-planet interactions, the N-body problem becomes N − 1 decoupled sun-planet 2-body problems, and Kepler’s classical laws of planetary motion assert that the planets move on fixed ellipses. In this Keplerian approximation, all of the elliptical parameters (i.e. semimajor axes and eccentricities), as well as the mutual inclinations between the planes of the ellipses, are constants of motion. Of course when we consider the full N-body problem, by taking into account the gravitational attractions of the planets on one another, the Keplerian ellipses now vary slowly. A fundamental problem in Celestial Mechanics is to understand the effect of planet-planet interactions in the N-body problem: do these weak forces average out over time so that the planets perform near-elliptical motions, or do the small variations accumulate over time making the planets’ orbits deviate strongly from ellipses?
This question can be phrased colloquially as Is the Solar system stable? and it was called by M. Herman the oldest problem in dynamical systems [4]. Nowadays it is known that the answer to this question is rather nuanced, and that, generally speaking, stable and unstable motions coexist.
This problem has attracted a tremendous amount of attention over the centuries. In the direction of stability, a series of increasingly strong arguments of Laplace, Lagrange and others throughout the XIX century indicated stability of the semimajor axes of planets’ orbits. This culminated in what has come to be known as the first stability theorem of Laplace and Lagrange: variations in the semimajor axes have zero average over certain time scales. Further to this, the classical Kolmogorov-Arnold-Moser Theory ensures that there exists a positive measure set of initial conditions whose orbits perform approximately for all time near-circular near-coplanar Keplerian ellipses.
Results concerning unstable motions in the N -body problem, however, are scarce. Instability, in this context, is represented by the existence of orbits along which nearly constant quantities drift a large amount over long time periods. In 1964, Arnold published a note, in which he proved that a specific near-integrable Hamiltonian system possesses orbits along which a constant of motion of the integrable approximation drifts a distance independent of the size of the perturbation [1]. In a footnote of that paper he wrote “I believe that the mechanism of ‘transition chains’ which guarantees that nonstability in our example is also applicable to the general case (for example, to the problem of three bodies).” This statement is now referred to as Arnold’s conjecture, and the phenomenon is called Arnold diffusion.
In the setting of the planetary problem, Arnold diffusion can be understood as the existence of orbits along which the interactions between planets cause the elliptical parameters to drift significant distances. Prior to the work described in this article, there have been no complete analytical proofs of Arnold diffusion in a planetary problem, and the existing picture has been one of stability.
In [2, 3], we construct the first example of unstable motion in the planetary problem. We consider the planetary 4-body problem and we assume that the semimajor axes of the Keplerian ellipses are of different orders, meaning that planet 2 is much farther from planet 1 than planet 1 is from the sun, whereas planet 3 is revolving even further away. Furthermore, we make the crucial assumption that the mutual inclination between the ellipses of planets 1 and 2 is large: we need it to be more than 55◦. Under these assumptions, we prove the following theorem.
Theorem. There exist orbits of the planetary 4-body problem along which:
- The eccentricity e_{2} of the orbital ellipse of planet 2 follows any finite predetermined itinerary with arbitrary precision.
- The mutual inclination i_{23} between the orbital planes of planets 2 and 3 follows any finite predetermined itinerary with arbitrary precision.
- The semimajor axis a_{3} of planet 3 follows any finite predetermined itinerary with arbitrary precision.
Observe that all of these quantities, e_{2}, i_{23}, a_{3} are constants of motion in the Keplerian approximation, and so this phenomenon is an instance of Arnold diffusion.
The motion in e_{2} described by part 1 of the theorem implies that, if we choose any η > 0 and any finite sequence 
here exists an orbit of the 4-body problem and times 0 < t_{1} < · · · < t_{N} , such that at time t_{j} the eccentricity e_{2}(t_{j}) of planet 2 satisfies 
. In particular, we can make the orbit start close to circular (i.e.
e_{2} ∼ 0), and at some point in the future, it can become highly eccentric (e_{2} ∼ 1).
Moreover, if we choose any finite sequence
⊂ T, we can find orbits of the 4-body problem such that, at time t_{j}, the mutual inclination i_{23}(t_{j}) between the orbital planes of planets 2 and 3 satisfies 
. For example, there are orbits where planets 2 and 3 start on almost coplanar Keplerian ellipses, going in the same direction (i.e. prograde motion), but then at some point in the future, the orbital plane of planet 2 can flip over so that again, planets 2 and 3 are almost coplanar but are now revolving in opposite directions (retrograde motion). Indeed, there are orbits where planet 2 flips over and back between prograde and retrograde motions arbitrarily many times.
Finally, and perhaps most curiously, if we choose any finite sequence 
, we can find orbits of the 4-body problem such that the semimajor axis a_{3}(t_{j}) of the outermost planet at time t_{j} satisfies 
. Along such orbits, the semimajor axis of planet 3 can grow to any predetermined size from its starting point, and indeed can oscillate. This is contrary to the findings of Laplace and Lagrange.
With regards to the title of this piece (as well as the title of [2]), we conjecture that this diffusion mechanism will likely lead to collisions in any solar system in which the inner planets are inclined. This is not proved in our work, as our analysis is valid away from collisions. Note, moreover, that our results do not apply to our own solar system, as the planets’ orbital ellipses are almost coplanar.
We point out that these phenomena described in parts 1-3 of the Theorem occur simultaneously along the same orbits. This constitutes the first analytical proof of Arnold’s conjecture in a planetary problem.
References
[1] V. I. Arnold, Instability of dynamical systems with many degrees of freedom, Dokl. Akad. Nauk SSSR 156 (1964), no. 1, 9-12. zbMath review.
[2] A. Clarke, J. Fejoz, and M. Guàrdia, Why are inner planets not inclined?, 2022. arXiv pdf.
[3] ___, A counterexample to the theorem of Laplace-Lagrange on the stability of semimajor axes, 2023. arXiv pdf.
[4] M. Herman, Some open problems in dynamical systems, Proceedings of the International Congress of Mathematicians, 1998, pp. 797-808. Volume pdf.