 Franco Coltraro defended his PhD thesis Robotic manipulation of cloth: mechanical modeling and perception, supervised by Professors Jaume Amorós and Maria Alberich-Carramiñana, on March 30th, 2023 within the UPC doctoral program in Applied Mathematics. Currently, he is a postdoctoral researcher at the Institut de Robòtica i Informàtica Industrial (IRI), CSIC-UPC in Barcelona.
Franco Coltraro defended his PhD thesis Robotic manipulation of cloth: mechanical modeling and perception, supervised by Professors Jaume Amorós and Maria Alberich-Carramiñana, on March 30th, 2023 within the UPC doctoral program in Applied Mathematics. Currently, he is a postdoctoral researcher at the Institut de Robòtica i Informàtica Industrial (IRI), CSIC-UPC in Barcelona.
Thesis summary
We introduce a new cloth model for the dynamics of textiles as inextensible surfaces. This assumption challenges most models in literature where elasticity is allowed, sometimes by necessity (Textile Engineering) or in the pursuit of spectacularity (Computer Graphics). Inextensibility is modeled as follows: we assume that our cloth S is a surface (with boundary) moving through space whose metric (first fundamental form) is preserved. In order to implement these conditions (which are in fact PDE’s) on a computer, we assume that S has been triangulated (or quadrangulated) and then apply a novel and non-trivial Finite Element discretization to the inextensibility constraints [1]. If we denote by φ(t) the position of the nodes of the polyhedron, this gives raise to a smooth (actually quadratic) constraint function C(φ) = 0 which must be preserved at all times. Making use of Signorini’s contact model, the dynamic equations of motion then would be:
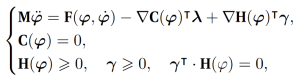
where we have grouped in the force term F damping, gravity, stiffness, aerodynamics, friction, etc. On the other hand, H(φ) ⩾ 0 contains the implicit equation of a given obstacle (e.g. a table) and in addition self-collision constraints. Since the collision and inextensibility forces turn out to be very stiff, the system must be integrated implicitly. This is done by solving a sequence of quadratic problems with linear constraints (basically by linearizing all non-linearities in the equation above). In order to solve these quadratic programs efficiently, we develop a novel active-set numerical algorithm which takes into account which constraints were active from one iteration to the next [2]. To our knowledge, our method is the first that results in a non-decoupled resolution of contacts, friction and inextensibility for cloth simulation in a single pass.
The inextensibility assumption is shown to be realistic by comparing simulations to experimental data: we record in a laboratory setting —with depth cameras and motion capture systems— the motions of seven types of textiles (including e.g. cotton, denim and polyester) of various sizes and at different speeds and end up with more than 80 recordings. The scenarios considered are all dynamic and involve rapid shaking and twisting of the textiles, collisions with frictional objects and even strong hits with a long stick. Then we compare the recorded textiles with the simulations given by our inextensible model and find that on average the mean error is of the order of 1 cm even for the largest sizes (DIN A2) and the most challenging scenarios [1, 2].
Furthermore, we also tackle other relevant problems to robotic cloth manipulation such as cloth perception and classification of its states. We present a reconstruction algorithm based on Morse theory that proceeds directly from a point-cloud to obtain a cellular decomposition of a surface with or without boundary: the results are a piecewise parametrization of the cloth surface as a union of Morse cells. From the cellular decomposition, the topology of the surface can be then deduced immediately [3]. Finally, we study the configuration space of a piece of cloth: since the original state of a piece of cloth is flat, the set of possible states under the inextensible assumption is the set of developable surfaces isometric to a fixed one. We prove that a generic simple, closed, piecewise regular curve in space can be the boundary of only finitely many developable surfaces with nonvanishing mean curvature [4]. Inspired by this result we introduce the dGLI cloth coordinates, a low-dimensional representation of the state of a piece of cloth based on a directional derivative of the Gauss Linking Integral. These coordinates —computed from the position of the cloth’s boundary— allow us to distinguish key qualitative changes in folding sequences [5].
Selected Publication: [1].
References
[1] F. Coltraro, J. Amorós, M. Alberich-Carramiñana and C. Torras: An inextensible model for the robotic manipulation of textiles. Applied Mathematical Modelling, Vol. 101 (2022), pp 832-858. pdf.
[2] F. Coltraro, J. Amorós, M. Alberich-Carramiñana and C. Torras: A novel collision model for inextensible textiles and its experimental validation. Under review. Preprint.
[3] M. Alberich-Carramiñana, J. Amorós, F. Coltraro, C. Torras, and M. Verdaguer: Morse cell decomposition and parametrization of surfaces from point-clouds. To appear in Proceedings of XVII EACA 2022 (Encuentro Álgebra Computacional y Aplicaciones), pp 33-36.
[4] M. Alberich-Carramiñana, J. Amorós and F. Coltraro. Developable surfaces with prescribed boundary. Trends in Mathematics, vol 15, pp. 127-132. Springer-Birkhäuser, 2021.
[5] F. Coltraro, J. Fontana, J. Amorós, M. Alberich-Carramiñana, J. Borràs and C. Torras: A Representation of Cloth States based on a Derivative of the Gauss Linking Integral. Accepted for publication in Applied Mathematics and Computation. Preprint.